Вариант 6 — различия между версиями

Материал из SimHardWiki
Перейти к: навигация, поиск
м (→‎Заключение)
 
(не показаны 17 промежуточных версий 2 участников)
Строка 1: Строка 1:
 
= Синтез логических устройств для реализации симметрических булевых функций =
 
= Синтез логических устройств для реализации симметрических булевых функций =
−
 
 
== Введение ==
 
== Введение ==
 +
При проектировании вычислительных устройств (ВУ) возникает задача реализации на одном логическом модуле (устройстве) всех булевых функций, принадлежащих определенному классу. В качестве такого класса весьма часто используется класс симметрических булевых функций (или некоторые из его подклассов). Интерес к симметрическим булевым функциям объясняется тем, что такими булевыми функциями описываются структура и поведение многих типовых устройств вычислительной техники [1].<br />
 +
К настоящему времени имеется довольно-таки много результатов в области синтеза универсальных логических модулей, а также в области синтеза многофункциональных логических модулей - устройств для вычисления произвольных , фундаментальных и полиномиально-однородных симметрических булевых функций [2, 3, 4].
  
−
При проектировании вычислительных устройств возникает задача реализации на одном логическом устройстве всех булевых функций,принадлежащих определенному классу. В качестве такого класса часто используется класс симметрических булевых функций или некоторые его подклассы. Интерес к симметрическим булевым функциям объясняется тем, что такими булевыми функциями описываются структура и поведение многих типовых устройств вычислительной техники [1].
 
−
К настоящему времени имеется довольно-таки много результатов в области синтеза устройств для вычисления произвольных симметрических булевых функций [2, 3], а также для вычисления фундаментальных [4] и полиномиально-однородных [5] симметрических булевых функций.
 
 
== Основные понятия теории булевых функций ==
 
== Основные понятия теории булевых функций ==
−
[[Файл:1284750149 2.jpg|обрамить|справа|булева алгебра]]
+
[[Файл:images (1).png|thumb|right|top|дипломная работа]]
 +
 
 
Среди функций одной переменной <m>F=F(x)</m> наибольший интерес представляет функция <m>F(x)=¬x</m> – '''''отрицание (инверсия)''''' переменной. Такая функция называется '''''элементарной''''' булевой функцией одной переменной.
 
Среди функций одной переменной <m>F=F(x)</m> наибольший интерес представляет функция <m>F(x)=¬x</m> – '''''отрицание (инверсия)''''' переменной. Такая функция называется '''''элементарной''''' булевой функцией одной переменной.
 
Кроме функции <m>F(x)=¬x</m> к числу элементарных относится 7 булевых функций, зависящих от двух переменных <m>x_1</m> и <m>x_2</m> :
 
Кроме функции <m>F(x)=¬x</m> к числу элементарных относится 7 булевых функций, зависящих от двух переменных <m>x_1</m> и <m>x_2</m> :
Строка 17: Строка 17:
 
* функция <m>F(x_1,x_2)=x_1 \setminus x_2</m> называется '''''штрих Шеффера'''''.
 
* функция <m>F(x_1,x_2)=x_1 \setminus x_2</m> называется '''''штрих Шеффера'''''.
 
<br />
 
<br />
 +
 +
[[Файл:1284750149 2.jpg|обрамить|справа|булева алгебра]]
 +
 +
 
{| cellspacing="0" cellpadding="10" border="1" class=standard
 
{| cellspacing="0" cellpadding="10" border="1" class=standard
 
|+Таблица истинности элементарных булевых функций двух переменных
 
|+Таблица истинности элементарных булевых функций двух переменных
Строка 70: Строка 74:
 
|}
 
|}
 
<br />
 
<br />
 +
 +
 +
 
'''Определение логической формулы:'''   
 
'''Определение логической формулы:'''   
 
# Булева переменная <m>x</m> является формулой.
 
# Булева переменная <m>x</m> является формулой.
Строка 76: Строка 83:
  
 
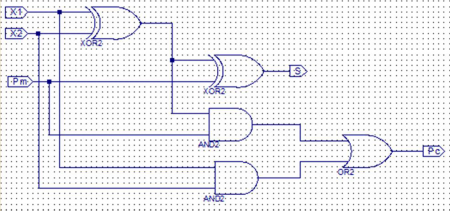
'''Пример.''' Описание двоичного сумматора на языке VHDL (x<sub>1</sub> и x<sub>2</sub> - соответствующие разряды суммируемых чисел, pm - перенос в данный разряд из соседнего младшего разряда суммы,s - соответствующий разряд суммы, pc - перенос в соседний старший разряд суммы) и соответствующая схемная реализация:
 
'''Пример.''' Описание двоичного сумматора на языке VHDL (x<sub>1</sub> и x<sub>2</sub> - соответствующие разряды суммируемых чисел, pm - перенос в данный разряд из соседнего младшего разряда суммы,s - соответствующий разряд суммы, pc - перенос в соседний старший разряд суммы) и соответствующая схемная реализация:
−
[[Файл:Безымянный.png|400px|thumb|left|схема сумматора]]
+
[[Файл:Безымянный.png|450px|thumb|left|схема сумматора]]
−
<big><source lang="vhdl">entity summator is
+
 
 +
 
 +
 
 +
<big><source lang="vhdl">
 +
 +
entity summator is
 
Port ( x1 : in STD_LOGIC;
 
Port ( x1 : in STD_LOGIC;
 
x2 : in STD_LOGIC;
 
x2 : in STD_LOGIC;
Строка 84: Строка 96:
 
pc : out STD_LOGIC);
 
pc : out STD_LOGIC);
 
end summator;
 
end summator;
 +
 
architecture Behavioral of summator is
 
architecture Behavioral of summator is
 
begin
 
begin
Строка 91: Строка 104:
 
pc<=((x1 and x2) or (x1 and pm) or (x2 and pm));
 
pc<=((x1 and x2) or (x1 and pm) or (x2 and pm));
 
end process;
 
end process;
−
end Behavioral;</source></big>
+
end Behavioral;
−
== Заключение ==
+
</source></big>
 +
<br />
  
−
Синтезированы устройства для вычисления самодвойственных симметрических булевых функции трех, пяти и семи переменных.
+
 
 +
{| class="wikitable"
 +
|+Таблица дат выполнения
 +
|-
 +
! Название глав дипломной работы !! Дата начала выполнения !! Дата конца выполнения
 +
|-
 +
| ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ БУЛЕВЫХ ФУНКЦИЙ || 13.04.2014 || 20.04.2014
 +
|-
 +
| КЛАССЫ БУЛЕВЫХ ФУНКЦИЙ || 21.04.2014 || 29.04.2014
 +
|-
 +
| ПОДКЛАССЫ СИММЕТРИЧЕСКИХ БУЛЕВЫХ ФУНКЦИЙ || 30.04.2014 || 10.05.2014
 +
|}
 +
 
 +
 
 +
<br />
 +
{| class="wikitable"
 +
|+Таблица отметок о выполнении
 +
|-
 +
! Название глав дипломной работы !! Отметка о выполнении
 +
|-
 +
| ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ БУЛЕВЫХ ФУНКЦИЙ || [[Файл:plus.png|20px|центр]]
 +
|-
 +
| КЛАССЫ БУЛЕВЫХ ФУНКЦИЙ || [[Файл:plus.png|20px|центр]]
 +
|-
 +
| ПОДКЛАССЫ СИММЕТРИЧЕСКИХ БУЛЕВЫХ ФУНКЦИЙ || [[Файл:plus.png|20px|центр]]
 +
|-
 +
| СХЕМНАЯ РЕАЛИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ || [[Файл:minus.jpg|20px|центр]]
 +
|-
 +
| СХЕМНАЯ РЕАЛИЗАЦИЯ СИММЕТРИЧЕСКИХ БУЛЕВЫХ ФУНКЦИЙ || [[Файл:minus.jpg|20px|центр]]
 +
|}
 +
<br />
 +
 
 +
 
 +
 
 +
 
 +
<graph >
 +
digraph "Граф задания на дипломную работу" {
 +
"Синтезировать устройства для реализации симметрических булевых функций" [shape=box]
 +
"Синтезировать устройства для реализации самодвойственных симметрических булевых функций" [shape=box]
 +
"Синтезировать устройства для реализации полиномиально-однородных симметрических булевых функций" [shape=box]
 +
"Оформить дипломную работу" [shape=diamond]
 +
"Изучить свойства симметрических булевых функций"  -> "Изучить свойства подклассов симметрических булевых функций" -> "Синтезировать устройства для реализации симметрических булевых функций" -> "Синтезировать устройства для реализации самодвойственных симметрических булевых функций" -> "Синтезировать устройства для реализации полиномиально-однородных симметрических булевых функций" -> "Оформить дипломную работу";
 +
}
 +
</graph>
 +
 
 +
== Заключение ==
 +
Мною были синтезированы логические устройства, на единственном выходе которых вычисляется (реализуется) произвольная симметрическая булева функция, зависящая от трех, четырёх и пяти, со сложной настройкой.
 +
Эти двухуровневые схемы имеют низкую конструктивную сложность (по числу входов логических элементов) и содержат относительно небольшое число внешних выводов.<br />
 +
'''СПИСОК ЛИТЕРАТУРЫ'''<br />
 +
[1] [[Media:Glushkov V.M. Sintez cifrovyh avtomatov (FML, 1962)(ru)(L)(T)(238s) CsNp .djvu|Математическая логика]] <br />
 +
[2] http://www.findpatent.ru<br />
 +
[3] http://www.belgospatent.org.by/database/index.php?pref=inv&lng=ru&page=1<br />
 +
[4] http://patentdb.su<br />

Текущая версия на 19:32, 16 декабря 2013

Содержание

Синтез логических устройств для реализации симметрических булевых функций

Введение

При проектировании вычислительных устройств (ВУ) возникает задача реализации на одном логическом модуле (устройстве) всех булевых функций, принадлежащих определенному классу. В качестве такого класса весьма часто используется класс симметрических булевых функций (или некоторые из его подклассов). Интерес к симметрическим булевым функциям объясняется тем, что такими булевыми функциями описываются структура и поведение многих типовых устройств вычислительной техники [1].
К настоящему времени имеется довольно-таки много результатов в области синтеза универсальных логических модулей, а также в области синтеза многофункциональных логических модулей - устройств для вычисления произвольных , фундаментальных и полиномиально-однородных симметрических булевых функций [2, 3, 4].

Основные понятия теории булевых функций

дипломная работа

Среди функций одной переменной наибольший интерес представляет функция – отрицание (инверсия) переменной. Такая функция называется элементарной булевой функцией одной переменной. Кроме функции к числу элементарных относится 7 булевых функций, зависящих от двух переменных и  :

  • функция называется конъюнкцией (или логическим умножением);
  • функция называется сложение по модулю два;
  • функция называется дизъюнкцией (или логическим сложением);
  • функция называется стрелкой Пирса (или функцией Вебба);
  • функция называется эквивалентностью;
  • функция называется импликацией ( посылка (основание), заключение (следствие));
  • функция называется штрих Шеффера.


булева алгебра


Таблица истинности элементарных булевых функций двух переменных
x1 x2 F1 F2 F3 F4 F5 F6 F7
0 0 0 0 0 1 1 1 1
0 1 0 1 1 0 0 1 1
1 0 0 1 1 0 0 0 1
1 1 1 0 1 0 1 1 0



Определение логической формулы:

  1. Булева переменная является формулой.
  2. Если и - формулы, то конструкции , , , , , , - также формулы.
  3. Других формул, кроме формул, перечисленных в п.1 и п.2, нет.
Пример. Описание двоичного сумматора на языке VHDL (x1 и x2 - соответствующие разряды суммируемых чисел, pm - перенос в данный разряд из соседнего младшего разряда суммы,s - соответствующий разряд суммы, pc - перенос в соседний старший разряд суммы) и соответствующая схемная реализация:
схема сумматора


 
entity summator is
Port ( x1 : in STD_LOGIC;
x2 : in STD_LOGIC;
pm : in STD_LOGIC;
s : out STD_LOGIC;
pc : out STD_LOGIC);
end summator;
 
architecture Behavioral of summator is
begin
process (x1,x2,pm)
begin
s<=(x1 xor x2 xor pm);
pc<=((x1 and x2) or (x1 and pm) or (x2 and pm));
end process;
end Behavioral;


Таблица дат выполнения
Название глав дипломной работы Дата начала выполнения Дата конца выполнения
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ БУЛЕВЫХ ФУНКЦИЙ 13.04.2014 20.04.2014
КЛАССЫ БУЛЕВЫХ ФУНКЦИЙ 21.04.2014 29.04.2014
ПОДКЛАССЫ СИММЕТРИЧЕСКИХ БУЛЕВЫХ ФУНКЦИЙ 30.04.2014 10.05.2014



Таблица отметок о выполнении
Название глав дипломной работы Отметка о выполнении
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ БУЛЕВЫХ ФУНКЦИЙ
Plus.png
КЛАССЫ БУЛЕВЫХ ФУНКЦИЙ
Plus.png
ПОДКЛАССЫ СИММЕТРИЧЕСКИХ БУЛЕВЫХ ФУНКЦИЙ
Plus.png
СХЕМНАЯ РЕАЛИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ
Minus.jpg
СХЕМНАЯ РЕАЛИЗАЦИЯ СИММЕТРИЧЕСКИХ БУЛЕВЫХ ФУНКЦИЙ
Minus.jpg




[svg]

Заключение

Мною были синтезированы логические устройства, на единственном выходе которых вычисляется (реализуется) произвольная симметрическая булева функция, зависящая от трех, четырёх и пяти, со сложной настройкой. Эти двухуровневые схемы имеют низкую конструктивную сложность (по числу входов логических элементов) и содержат относительно небольшое число внешних выводов.
СПИСОК ЛИТЕРАТУРЫ
[1] Математическая логика
[2] http://www.findpatent.ru
[3] http://www.belgospatent.org.by/database/index.php?pref=inv&lng=ru&page=1
[4] http://patentdb.su

Источник — «http://simhard.com/ex/index.php?title=Вариант_6&oldid=185»