Вариант 6 — различия между версиями
Korobko (обсуждение | вклад) |
Korobko (обсуждение | вклад) |
||
| Строка 75: | Строка 75: | ||
# Других формул, кроме формул, перечисленных в п.1 и п.2, нет. | # Других формул, кроме формул, перечисленных в п.1 и п.2, нет. | ||
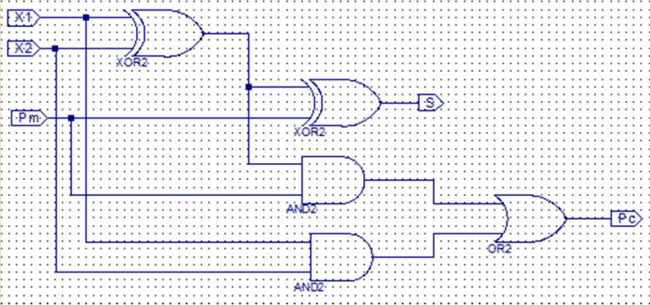
| − | '''Пример.''' Описание двоичного сумматора на языке VHDL (x<sub>1</sub> и x<sub>2</sub> - соответствующие разряды суммируемых чисел, pm - перенос в данный разряд из соседнего младшего разряда суммы,s - соответствующий разряд суммы, pc - перенос в соседний старший разряд суммы): | + | '''Пример.''' Описание двоичного сумматора на языке VHDL (x<sub>1</sub> и x<sub>2</sub> - соответствующие разряды суммируемых чисел, pm - перенос в данный разряд из соседнего младшего разряда суммы,s - соответствующий разряд суммы, pc - перенос в соседний старший разряд суммы) и соответствующая схемная реализация: |
| − | + | [[Файл:Безымянный.png|650px|слева|схема сумматора]] | |
<big><source lang="vhdl">entity summator is | <big><source lang="vhdl">entity summator is | ||
Port ( x1 : in STD_LOGIC; | Port ( x1 : in STD_LOGIC; | ||
Версия 17:22, 23 ноября 2013
Содержание |
Синтез логических устройств для реализации симметрических булевых функций
Введение
При проектировании вычислительных устройств возникает задача реализации на одном логическом устройстве всех булевых функций,принадлежащих определенному классу. В качестве такого класса часто используется класс симметрических булевых функций или некоторые его подклассы. Интерес к симметрическим булевым функциям объясняется тем, что такими булевыми функциями описываются структура и поведение многих типовых устройств вычислительной техники [1]. К настоящему времени имеется довольно-таки много результатов в области синтеза устройств для вычисления произвольных симметрических булевых функций [2, 3], а также для вычисления фундаментальных [4] и полиномиально-однородных [5] симметрических булевых функций.
Основные понятия теории булевых функций
Среди функций одной переменной наибольший интерес представляет функция – отрицание (инверсия) переменной. Такая функция называется элементарной булевой функцией одной переменной. Кроме функции к числу элементарных относится 7 булевых функций, зависящих от двух переменных и :
- функция называется конъюнкцией (или логическим умножением);
- функция называется сложение по модулю два;
- функция называется дизъюнкцией (или логическим сложением);
- функция называется стрелкой Пирса (или функцией Вебба);
- функция называется эквивалентностью;
- функция называется импликацией ( посылка (основание), заключение (следствие));
- функция называется штрих Шеффера.
| x1 | x2 | F1 | F2 | F3 | F4 | F5 | F6 | F7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
Определение логической формулы:
- Булева переменная является формулой.
- Если и - формулы, то конструкции , , , , , , - также формулы.
- Других формул, кроме формул, перечисленных в п.1 и п.2, нет.
entity summator is Port ( x1 : in STD_LOGIC; x2 : in STD_LOGIC; pm : in STD_LOGIC; s : out STD_LOGIC; pc : out STD_LOGIC); end summator; architecture Behavioral of summator is begin process (x1,x2,pm) begin s<=(x1 xor x2 xor pm); pc<=((x1 and x2) or (x1 and pm) or (x2 and pm)); end process; end Behavioral;
Заключение
Синтезированы устройства для вычисления самодвойственных симметрических булевых функции трех, пяти и семи переменных.