Вариант 6

Ссылки сюда (1) →

Синтез логических устройств для реализации симметрических булевых функций

Введение

При проектировании вычислительных устройств (ВУ) возникает задача реализации на одном логическом модуле (устройстве) всех булевых функций, принадлежащих определенному классу. В качестве такого класса весьма часто используется класс симметрических булевых функций (или некоторые из его подклассов). Интерес к симметрическим булевым функциям объясняется тем, что такими булевыми функциями описываются структура и поведение многих типовых устройств вычислительной техники [1]. К настоящему времени имеется довольно-таки много результатов в области синтеза универсальных логических модулей, а также в области синтеза многофункциональных логических модулей - устройств для вычисления произвольных [2], фундаментальных [3] и полиномиально-однородных [4] симметрических булевых функций.

Основные понятия теории булевых функций

дипломная работа

Среди функций одной переменной наибольший интерес представляет функция – отрицание (инверсия) переменной. Такая функция называется элементарной булевой функцией одной переменной. Кроме функции к числу элементарных относится 7 булевых функций, зависящих от двух переменных и  :

• функция называется конъюнкцией (или логическим умножением);
• функция называется сложение по модулю два;
• функция называется дизъюнкцией (или логическим сложением);
• функция называется стрелкой Пирса (или функцией Вебба);
• функция называется эквивалентностью;
• функция называется импликацией ( посылка (основание), заключение (следствие));
• функция называется штрих Шеффера.

булева алгебра

Таблица истинности элементарных булевых функций двух переменных

x1	x2	F1	F2	F3	F4	F5	F6	F7
0	0	0	0	0	1	1	1	1
0	1	0	1	1	0	0	1	1
1	0	0	1	1	0	0	0	1
1	1	1	0	1	0	1	1	0

Определение логической формулы:

1. Булева переменная является формулой.
2. Если и - формулы, то конструкции , , , , , , - также формулы.
3. Других формул, кроме формул, перечисленных в п.1 и п.2, нет.

Пример. Описание двоичного сумматора на языке VHDL (x₁ и x₂ - соответствующие разряды суммируемых чисел, pm - перенос в данный разряд из соседнего младшего разряда суммы,s - соответствующий разряд суммы, pc - перенос в соседний старший разряд суммы) и соответствующая схемная реализация:

схема сумматора

 
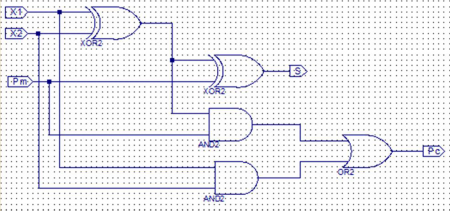
entity summator is
Port ( x1 : in STD_LOGIC;
x2 : in STD_LOGIC;
pm : in STD_LOGIC;
s : out STD_LOGIC;
pc : out STD_LOGIC);
end summator;
 
architecture Behavioral of summator is
begin
process (x1,x2,pm)
begin
s<=(x1 xor x2 xor pm);
pc<=((x1 and x2) or (x1 and pm) or (x2 and pm));
end process;
end Behavioral;

Таблица дат выполнения

Название глав дипломной работы	Дата начала выполнения	Дата конца выполнения
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ БУЛЕВЫХ ФУНКЦИЙ	13.04.2014	20.04.2014
КЛАССЫ БУЛЕВЫХ ФУНКЦИЙ	21.04.2014	29.04.2014
ПОДКЛАССЫ СИММЕТРИЧЕСКИХ БУЛЕВЫХ ФУНКЦИЙ	30.04.2014	10.05.2014

Таблица отметок о выполнении

Название глав дипломной работы	Отметка о выполнении
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ БУЛЕВЫХ ФУНКЦИЙ
КЛАССЫ БУЛЕВЫХ ФУНКЦИЙ
ПОДКЛАССЫ СИММЕТРИЧЕСКИХ БУЛЕВЫХ ФУНКЦИЙ
СХЕМНАЯ РЕАЛИЗАЦИЯ БУЛЕВЫХ ФУНКЦИЙ
СХЕМНАЯ РЕАЛИЗАЦИЯ СИММЕТРИЧЕСКИХ БУЛЕВЫХ ФУНКЦИЙ

Заключение

Синтезированы устройства для вычисления самодвойственных симметрических булевых функции трех, пяти и семи переменных.
СПИСОК ЛИТЕРАТУРЫ
[1] Файл:Карцев М.А. Арифметика цифровых машин. – М. Наука, 1969..pdf
[2] Фридман А., Менон П. Теория и проектирование переключательных схем. – М.: Мир, 1978.
[3] Артюхов В.Л., Копейкин Г.Н., Шалыто А.А. Настраиваемые модули для управляющих логических устройств. – Л.: Энергоиздат, 1981. [5] Супрун В.П., Седун А.М. Метод двухуровневой схемной реализации симметрических булевых функций // Материалы Второй международной конференции "Автоматизация проектирования дискретных систем" (CAD DD’97), Минск, 12 – 14 ноября 1997 г., т. 2, с. 6 – 11. [6] Седун А.М., Супрун В.П. Реализация симметрических булевых функций посредством логических устройств со сложной настройкой // Труды Пятой международной конференции «Новые информационные технологии» (NITe’2002), Минск, 29 – 31 октября 2002 г., с. 116 – 120. [7] Супрун В.П., Седун А.М. Схемная реализация фундаментальных симметрических булевых функций посредством логических устройств со сложной настройкой // Материалы Четвертой международной конференции "Автоматизация проектирования дискретных систем" (CAD DD’01), Минск, 14 – 17 ноября 2001 г., т. 2, с. 86 – 91. [8] Супрун В.П. Синтез логических устройств для вычисления полиномиально-однородных симметрических булевых функций // Материалы Шестой международной конференции "Автоматизация проектирования дискретных систем" (CAD DD’07), Минск, 14 – 15 ноября 2007 г., т. 2, с. 146 – 153.