Вариант 4
Содержание |
Синтез логических схем структурных автоматов Мили на элементах классического базиса
Введение
Не все окружающие нас преобразователи информации выполняют функциональное отражение информации. Результат преобразования вход=>выход зачастую зависит не только от того, какая информация в данный момент появилась на входе, но и от того, что происходило раньше, от предыстории преобразования. Множество примеров тому дают биологические системы. Например, один и тот же вход – извинение соседа после того, как он наступил вам на ногу в переполненном трамвае – вызовет у вас одну реакцию в первый раз и совсем другую – в пятый раз. По-видимому, ваша реакция будет различной, она будет зависеть от предыдущих событий, произошедших в трамвае, от входной истории. Таким образом, существуют более сложные, не функциональные преобразователи информации; их реакция зависит не только от входа в данный момент, но и от того, что было на входе раньше, от входной истории. Такие преобразователи называются автоматами. Исследования в области теории автоматов начались в середине 50-х годов прошлого века. Несмотря на свою простоту, модель конечного автомата оказалась чрезвычайно удобной в огромном числе приложений не только в информатике, но и в других областях инженерной деятельности. Большой интерес к этой теории объясняется именно широкими возможностями ее применения. Из выступлений на семинаре «Software 2000: a View of the Future» 10 апреля 1994 года: Brian Randell: «Я помню Дуга Росса из компании SofTech, много лет назад говорившего, что 80 или даже 90% информатики (Computer Science) будут в будущем основываться на теории конечных автоматов»[1]. Herve Gallaire: «Я знаю людей из «Боинга», занимающихся системами стабилизации самолетов с использованием чистой теории автоматов. Даже трудно себе представить, что им удалось сделать с помощью этой теории»[1]. Brian Randell: «Большая часть теории автоматов была успешно использована в системных программах и текстовых фильтрах в OS UNIX. Это позволяет множеству людей работать на высоком уровне и разрабатывать очень эффективные программы»[1]. Целью курсовой работы является разработка алгоритма перехода от абстрактного автомата Мили к структурному, написание программы совместной реализации функций выходов и переходов структурного автомата Мили, которая в будущем может быть использована в учебном процессе.
БУЛЕВА ФУНКЦИЯ
- Определение 1.1. Логическая (булева) переменная - такая величина x, которая может принимать только два значения: x = {0,1} (ложное или истинное высказывание).
- Определение 1.2. Логическая функция (функция алгебры логики – ФАЛ) – функция многих аргументов f(xn-1, xn-2,, ..., x0), принимающая значения равные нулю или единице на наборах логических переменных xn-1, xn-2,, ..., x0 [3].
Любую логическую функцию можно задать таблицей истинности, в левой части которой вписаны все возможные наборы значений ее аргументов x_1,x_2,…,x_n , а правая часть - столбец значений функции, соответствующих этим наборам.
Некоторые функции имеют специальные названия и значения. На их основе булеву функцию можно представить в виде формулы. Значения всех логических функций от одной переменной представлены в таблице 1.1.
Таблица 1.1. Значения логических функций
| x | fo(x) | f1(x) | f2(x) | f3(x) |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
Функция f0(x) называется константой нуля, а функция f1(x) - константой единицы.
Функция f2(x), повторяющая значения логической переменной, - тождественная функция (f2(x) = x), а функция f3(x), принимающая значения, обратные значениям переменной x, - логическое отрицание или инверсия (НЕ) (f3(x) = /x ).
В таблице 1.2 перечислены некоторые булевы функции от двух аргументов :
Таблица 1.2. Булевы функции
| x1x2 | g0 | g1 | g2 | g3 | g4 | g5 | g6 | g7 | g8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
Закон функционирования автоматов Мили описывается следующими выражениями для функции переходов и функции выходов:
В данных уравнениях a(t) – состояние автомата в момент времени t, z(t) и w(t) – входной и выходной сигналы в момент t, δ(a(t),z(t)) – функция переходов автомата, λ(a(t),z(t)) – функция выходов автомата [4].
Отличительной особенностью автоматов Мили является то, что их выходные сигналы зависят как от состояния автомата, так и от значения входного сигнала.
Для полного задания автомата Мили дополнительно к законам функционирования, необходимо указать их начальное состояние и определить входной и выходной алфавиты.
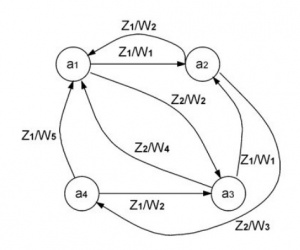
При графическом способе автомат задается в виде ориентированного графа, вершины которого соответствуют состояниям, а дуги – переходам между ними. Дуга, направленная из вершины am, задает переход в автомате из состояния am в состояние as. В начале этой дуги записывается входной сигнал zf∈ Z, вызывающий данный переход as=δ(am,zf). Для графа автомата Мили выходной сигнал wg ∈ W, формируемый на переходе, записывается в конце дуги. Если переход в автомате из состояния am в состояние as производится под действием нескольких входных сигналов, то дуге графа, направленной из am в as, приписываются все эти входные и соответствующие выходные сигналы. Граф автомата Мили представлен на рисунке 2.2 [4].
Function minm(ByRef lm, ByRef skleika, ByRef n) Dim fl For i1 = 1 To lm - 1 For i2 = i1 + 1 To lm fl = 0 For j = 1 To n If skleika(i1, j) = skleika(i2, j) Then fl = fl + 1 End If Next If fl = n Then For i3 = i2 + 1 To lm For j = 1 To n skleika(i3 - 1, j) = skleika(i3, j) Next Next lm = lm - 1 End If Next Next End Function
Заключение
При выполнении курсовой работы был рассмотрен алгоритм перехода от абстрактного автомата Мили к структурному, написана программа совместной реализации функций переходов и выходов структурного автомата Мили.
В дальнейшем возможно увеличение исходной таблицы абстрактного автомата Мили, возможность работы с частичными автоматами, и окончательная реализация схем. Также имеется возможность нахождение оптимального алгоритма кодировки алфавитов исходного автомата и нахождение зависимости числа строк итоговой таблицы от числа входных параметров.
СПИСОК ЛИТЕРАТУРЫ