Вариант 5
Содержание |
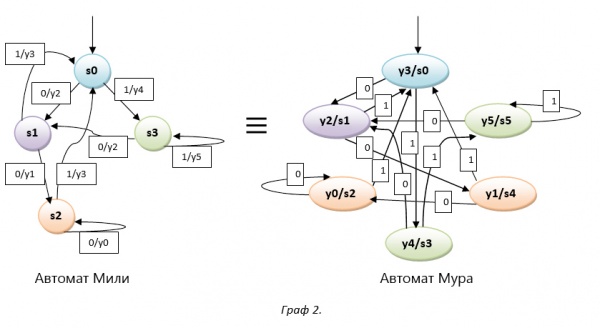
Структурные автоматы. Минимизация, кодировка и матричная реализация
Введение
Не все окружающие нас преобразователи информации выполняют функциональное отражение информации. Результат преобразования вход=>выход зачастую зависит не только от того, какая информация в данный момент появилась на входе, но и от того, что происходило раньше, от предыстории преобразования. Множество примеров тому дают биологические системы. Например, один и тот же вход – извинение соседа после того, как он наступил вам на ногу в переполненном трамвае – вызовет у вас одну реакцию в первый раз и совсем другую – в пятый раз. По-видимому, ваша реакция будет различной, она будет зависеть от предыдущих событий, произошедших в трамвае, от входной истории. Таким образом, существуют более сложные, не функциональные преобразователи информации; их реакция зависит не только от входа в данный момент, но и от того, что было на входе раньше, от входной истории. Такие преобразователи называются автоматами. Исследования в области теории автоматов начались в середине 50-х годов прошлого века. Несмотря на свою простоту, модель конечного автомата оказалась чрезвычайно удобной в огромном числе приложений не только в информатике, но и в других областях инженерной деятельности. Большой интерес к этой теории объясняется именно широкими возможностями ее применения.
Основные понятия алгебры логики
Понятие цифрового автомата было введено как модель для описания функционирования устройств, предназначенных для переработки цифровой или дискретной информации. Для формального описания цифровых автоматов применяется аппарат алгебры логики, созданной английским математиком Джорджем Булем (1815-1864). Поэтому алгебру логики называют алгеброй Буля или булевой алгеброй. В алгебре логики применительно к описанию цифровых автоматов, работающих в двоичном представлении кодов (или цифровой информации) основными понятиями являются логическая (булева) переменная и логическая функция (функция алгебры логики - ФАЛ).
- Определение 1.1. Логическая (булева) переменная - такая величина x, которая может принимать только два значения: x = {0,1} (ложное или истинное высказывание) [3].
- Определение 1.2. Логическая функция (функция алгебры логики – ФАЛ) – функция многих аргументов f(xn-1, xn-2,, ..., x0), принимающая значения равные нулю или единице на наборах логических переменных xn-1, xn-2,, ..., x0 [3].
В дальнейшем в формальных описаниях наборов переменных и логических функций сами наборы переменных интерпретируются как двоичные коды (числа). В двоичных кодах расположение логических переменных упорядочено в порядке уменьшения индекса слева направо и каждая логическая переменная имеет вес в зависимости от позиции в коде, увеличивающийся справа налево. Вес каждой i - той логической переменной, являющейся значением разряда двоичного числа равен 2i (i = 0, ... , n-1). Для n - разрядного кода общее количество уникальных наборов переменных N = 2n; Максимальное числовое значение двоичного кода равно Aмакс = 2n-1; Значения всех логических функций от одной переменной представлены в таблице 1.1.
Таблица 1.1. Значения логических функций
| x | fo(x) | f1(x) | f2(x) | f3(x) |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
Функция f0(x) называется константой нуля, а функция f1(x) - константой единицы. Функция f2(x), повторяющая значения логической переменной, - тождественная функция (f2(x) = x), а функция f3(x), принимающая значения, обратные значениям переменной x, - логическое отрицание или инверсия (НЕ) (f3(x) = /x ). В таблице 1.2 перечислены некоторые булевы функции от двух аргументов :
Таблица 1.2. Булевы функции
| x1x2 | g0 | g1 | g2 | g3 | g4 | g5 | g6 | g7 | g8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
- g0(x1,x2) = 0 - константа 0
- g1(x1,x2) = 1 - константа 1
- g2(x1,x2) = x1 x2 - дизъюнкция
- g3(x1,x2) = x1 x2 - конъюнкция
- g4(x1,x2) = x1 x2 - сложение по модулю 2
- g5(x1,x2) = x1 x2 - эквивалентность
- g6(x1,x2) = x1 x2 - импликация
- g7(x1,x2) = x1 x2 - стрелка Пирса
- g8(x1,x2) = x1 x2 - штрих Шеффера
Над элементами алгебры логики можно выполнять следующие операции:
- Определение 1.3. Конъюнкция (И, логическое умножение) – произведение двух высказываний Р и Q, результатом которого является истина если оба высказывания истинны и ложное во всех других случаях [4].
- Определение 1.4. Дизъюнкция (ИЛИ, логическая сумма) – сумма двух высказываний Р и Q, называется высказывание ложное если оба высказывания ложные и истинное во всех других случаях [4].
- Определение 1.5. Инверсия (отрицание) – отрицание высказывания Р называется высказывание истинное, когда само высказывание Р ложное или наоборот [4].
- Определение 1.6. Система булевых функций W называется функционально полной, если для любой булевой функции n - переменных f(xn-1, xn-2,, ..., x0) может быть построена равносильная ей функция комбинированием булевых переменных xn-1, xn-2,, ..., x0 и функций системы W, взятых в любом конечном количестве экземпляров каждая. Такая система булевых функций (W) называется базисом [3].
Таким образом, базис - полная система функций алгебры логики (ФАЛ), с помощью которой любая ФАЛ может быть представлена суперпозицией исходных функций W.
Базисом является система функций И (конъюнкция), ИЛИ (дизъюнкция), НЕ (инверсия), свойства которых были впервые изучены Дж. Булем.
Базисами являются системы: - И, НЕ; - ИЛИ, НЕ; - функция Шеффера И-НЕ; - функция Пирса ИЛИ-НЕ.
Базис является минимальным, если удаление из него хотя бы одной функции превращает систему ФАЛ в неполную. Базис И, ИЛИ, НЕ – избыточный [3].
- Определение 1.7. Программируемая логическая матрица (ПЛМ) представляет собой функциональный блок, созданный на базе полупроводниковой технологии и предназначенный для реализации логических схем цифровых систем [4].
- Определение 1.8. Программируемая логическая матрица (ПЛМ) представляет собой матрицу логических элементов, которую можно запрограммировать для выполнения сложных логических функций (комбинации дизъюнкций и конъюнкций) подачей установочной информации на определенные входы [4].
#include <vcl.h> #include <stdlib.h> #include <math.h> #include <string> #pragma hdrstop #include "Unit1.h" #include "Unit2.h" #pragma package(smart_init) #pragma resource "*.dfm" TForm1 *Form1; //Создаем вариант размещения без повторений из n по k int* allocation(int k) { randomize(); long n = powl(2, ceil(log(k)/log(2))); int *res = new int[n]; int *arr = new int[k]; for( int i = 0; i < n; i++ ) { res[i] = i; } for (int i = 0; i < k; i++) { int j = i + random(n-i); int t = res[i]; res[i] = res[j]; res[j] = t; } for (int i = 0; i < k; i++) { arr[i] = res[i]; } return arr;} void __fastcall TForm1::StringGrid2TopLeftChanged(TObject *Sender) {StringGrid2->Repaint();} AnsiString TForm1::IntToBinary(int value, int dimension) { String result, temp; for (int i = 0; i < dimension; i++) { int bit = (value & (1 << i)) > 0?1:0; temp += bit; } for (int i = 0; i < dimension; i++) result += temp[dimension-i]; return result;}
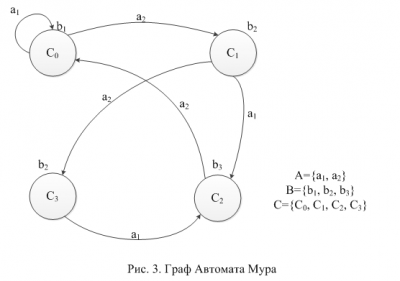
граф
Заключение
При выполнении курсовой работы был рассмотрен алгоритм перехода от абстрактного автомата Мили к структурному, рассмотрены различные кодировки, рассмотрена задача минимизации, реализован случай выбора наилучшей минимальной реализации для каждого вида кодировок, написана программа подсчета сложности матричной реализации автомата Мили. Можно сделать вывод, что в большинстве своем минимизация через хитрую кодировку более эффективна. В дальнейшем возможна работа с автоматом Мура, частичными автоматами.