Проектирование цифровых систем на языках описания аппаратуры/Лекция 9

Ссылки сюда (17) →

Лекции ПЦСЯОА

• Чеклист

---

Лекции

Лекция 1 Лекция 2 Лекция 3 Лекция 4 Лекция 5 Лекция 6 Лекция 7 Лекция 8 Лекция 9 Лекция 10 Лекция 11 Лекция 12

Лекция 13 Лекция 14 Лекция 15 Лекция 16 Лекция 17 Лекция 18 Лекция 19 Лекция 20 Лекция 21 Лекция 22 Лекция 23 Лекция 24

---

Практические

• Тест 1 - Основы VHDL
• Тест 2 - Вопросы по VHDL (простой уровень)

---

Доп. материалы

• Ссылки
• Книги
• Софт
  • Редактор Emacs
  • ModelSim
  • ISE
  • LeonardoSpectrum

---

• Форум
• Журнал
• План сдачи заданий
• Экзамен

Slide Show

Заголовок

Описание конечных автоматов и схем с памятью

Автор

Ланкевич Ю.Ю.

Нижний колонтитул

Проектирование цифровых систем на языках описания аппаратуры/Лекция 9

Дополнительный нижний колонтитул

Ланкевич Ю.Ю., 01:15, 12 октября 2020

Слайд:Определение конечного автомата

• Абстра́ктный автома́т (в теории алгоритмов) — математическая абстракция, модель дискретного устройства, имеющего один вход, один выход и в каждый момент времени находящегося в одном состоянии из множества возможных. На вход этому устройству поступают символы одного алфавита, на выходе оно выдаёт символы (в общем случае) другого алфавита.
  

Ограничение числа состояний абстрактного автомата определило такое понятие как конечный автомат. Конечный автомат K определяется как набор

K = (A, Z, W, δ , λ , a₁ ), где

• A = { a₁ ,..., a_Q } – множество (алфавит) состояний (имеются в виду внутренние состояния автомата);
• Z = { z₁ ,..., z_N } – множество входных сигналов (входной алфавит);
• W = { w₁ ,..., w_M } – множество выходных сигналов (выходной алфавит);
• δ – функция переходов, определяющая состояние автомата в момент времени t+1 в зависимости от состояния автомата и входного сигнала в момент времени t, иначе говоря,

a_s = δ (a_m , z), где

• a_m – состояние автомата в момент времени t;
• z – входной сигнал в момент времени t;
• a_s – состояние автомата в момент времени t+1;
• λ – функция выходов.

Слайд:Автомат Мили и автомат Мура

Если функция λ по состоянию автомата a_q и входному сигналу z_n определяет значение выходного сигнала w_m

w_m = λ (a_q , z_n )

то конечный автомат называется автоматом Мили , если же

w_m = λ (a),

то конечный автомат называется автоматом Мура;

• a₁ – начальное состояние автомата в момент времени t =0, a₁∈A.

Слайд:Автомат Мили

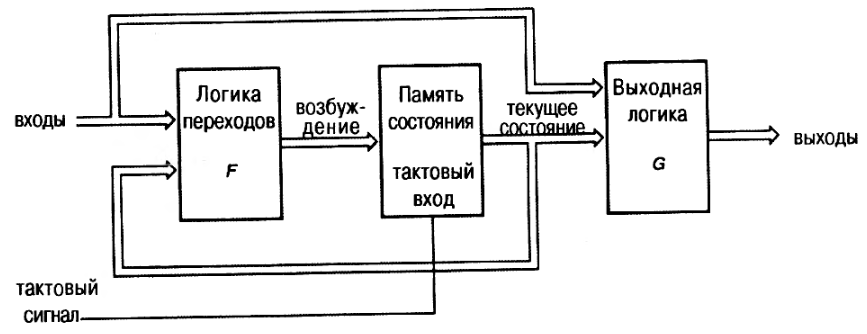
• Следующее состояние = F (текущее состояние, вход)
• Выход = G (текущее состояние, вход)

Слайд:Автомат Мура

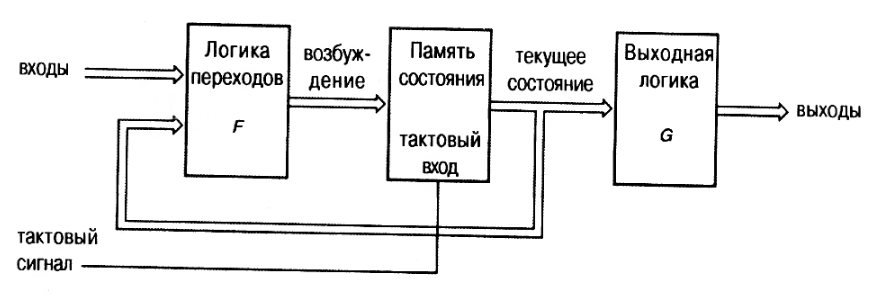
• Следующее состояние = F (текущее состояние, вход)
• Выход = G (текущее состояние)

Слайд: Литература по построению автоматов

• Потемкин И.С. Функциональные узлы цифровой автоматики. – 1988, 320 с.
• Д. Уэйкерли Пректирование цифровых устройств. В 2-х томах / Том 2 — М., 2002 Т. 2. — 536 с. – глава 7 посвящена проектированию автоматов.
• Бибило П.Н. Основы языка VHDL: Учебное пособие. – М.: Книжный дом «ЛИБРОКОМ», 2012. – 328 с. – Глава 4.3 посвящена описанию автоматов на VHDL

Слайд: Граф состояний и переходов

Кодирование выходов Состояние выхода Значение y[1:0] y1 00 y2 10 y3 11 Кодирование состояний Состояние Код Q1 0001 Q2 0010 Q3 0100 Q4 1000

Слайд: Выбор состояний для выходов и кодирование состояний

• Для хранения значения текущего состояния автомата используется 4-х разрядный регистр со сбросом в "0001" (код состояния Q1), который реализуется с помощью 4-х D-триггеров с асинхронными сбросом и установкой.

Слайд: Таблица переходов (таблица истинности логики переходов F)

• таблица переходов представляет собой альтернативную запись исходного графа

Текущее состояние state Входы автомата Следующее состояние next_state Код Имя x[2] x[1] Код Имя "0001" Q1 – '1' "0010" Q2 "0001" Q1 – '0' "0001" Q1 "0010" Q2 '1' '0' "0100" Q3 "0010" Q2 – '1' "1000" Q4 "0010" Q2 – '0' "0010" Q2 "1000" Q4 – '1' "0001" Q1 "1000" Q4 – '0' "1000" Q4 "0100" Q3 – – "0100" Q3

Обозначения в таблице:

• знак '–' - значение лог. '0' либо '1'

Слайд: Таблица истинности выходной логики G

Состояние State[3:0]		Выход y[1:0]
Имя	Код	Имя	Код
Q1	"0001"	y1	"00"
Q2	"0010"	y2	"10"
Q3	"0100"	y1	"00"
Q4	"1000"	y3	"11"

Слайд: VHDL-модель автомата

Вариант 1	Вариант 2	Вариант 3
library ieee; use ieee.std_logic_1164.all;   entity automat is   port ( x : in std_logic_vector(2 downto 1); rst : in std_logic; clk : in std_logic; y : out std_logic_vector(1 downto 0));   end automat;   architecture beh of automat is   signal state : std_logic_vector(3 downto 0); signal next_state : std_logic_vector(3 downto 0);   begin -- beh   -- Задание логики переходов (F) next_state <= "0010" when state="0001" and x(1)='1' else "0001" when state="0001" else "0100" when state="0010" and x(2 downto 1) = "10" else "1000" when state="0010" and x(1)='1' else "0010" when state="0010" else "0001" when state="1000" and x(1)='1' else "1000" when state="1000" else "0100" when state="0100" else "0000";   -- Задание выходной логики (G) y <= "00" when state="0001" else "10" when state="0010" else "00" when state="0100" else "11" when state="1000" else "00";   -- регистр, хранящий текущее состояние p1: process (clk, rst) begin -- process p1 if rst = '1' then state <= "0001"; elsif clk'event and clk = '1' then state <= next_state; end if; end process p1;   end beh;	architecture beh2 of automat is   type state_type is (Q1, Q2, Q3, Q4); signal state : state_type; signal next_state : state_type;   begin -- beh   c1: process (state, x) is begin -- process c1 case state is when Q1 => y <= "00"; if x(1)='1' then next_state <= Q2; else next_state <= Q1; end if; when Q2 => y <= "10"; if x = "10" then next_state <= Q3; elsif x(1) = '1' then next_state <= Q4; else next_state <= Q2; end if; when Q3 => y <= "00"; next_state <= Q3; when Q4 => y <= "11"; if x(1) = '1' then next_state <= Q1; else next_state <= Q4; end if; when others => null; end case; end process c1;   -- регистр, хранящий текущее состояние p1: process (clk, rst) begin -- process p1 if rst = '1' then state <= Q1; elsif clk'event and clk = '1' then state <= next_state; end if; end process p1;   end beh2;	architecture beh3 of automat is   type state_type is (Q1, Q2, Q3, Q4); signal state : state_type;   begin -- beh   p1: process (clk, rst) begin -- process p1 if rst = '1' then state <= Q1; elsif clk'event and clk = '1' then   if state = Q1 then if x(1)='1' then state <= Q2; end if;   elsif state = Q2 then   if x = "10" then state <= Q3; elsif x(1) = '1' then state <= Q4; end if;   elsif state = Q3 then   elsif state = Q4 then   if x(1) = '1' then state <= Q1; end if;   else -- защита от сбоя state <= Q1;   end if;   end if; end process p1; -- Задание выходной логики (G) y <= "00" when state = Q1 else "10" when state = Q2 else "00" when state = Q3 else "11" when state = Q4 else "00";   end beh3;

Слайд:Пример автомата Мили

Функционирование автомата происходит следующим образом: в дискретные моменты времени t = 0, 1, 2, 3,... на вход устройства поступает входной сигнал – один из элементов множества Z, а на выходе появляется выходной сигнал – один из элементов множества W, в этот же момент времени t автомат из состояния a_m переходит в состояние a_s, в котором он будет находиться в момент времени t+1.
Разработаны различные формы задания конечных автоматов. Например, в таблице задан конечный автомат Мили с четырьмя внутренними состояниями

Входные сигналы	Состояния
	a1	a2	a3	a4
z1	a2/w1	a2/w1	a1/w2	a1/w4
z2	a4/w5	a3/w3	a4/w4	a3/w5

Алфавит состояний A = {a₁, a₂, a₃, a₄}, q = 1,...,4. Входной алфавит Z образуют сигналы z₁, z₂, т.е. Z = {z₁ , z₂ }, n = 1,2. Выходной алфавит W образуют сигналы w₁, ..., w₅, т.е. W = {w₁,w₂,w₃,w₄,w₅}, m = 1,...,5. На пересечении строки z_n и столбца a_q в таблице находится состояние a_s , в которое должен перейти автомат из состояния a_q под воздействием сигнала z_n. После косой черты в этой же графе таблицы указывается выходной сигнал, выдаваемый автоматом в состоянии aq при поступлении на его вход сигнала z_n. Иначе говоря, выше представлена таблица задания функций δ , λ, которая называется совмещенной таблицей переходов и выходов.
Автомат может быть задан ориентированным графом, в котором вершинам соответствуют абстрактные внутренние состояния автомата, а дуги соответствуют переходам между состояниями. Такой граф носит название графа автомата. Для автомата, заданного в таблице, граф автомата имеет следующий вид.

Легко видеть, что совмещенная таблица переходов и выходов автомата и граф автомата являются эквивалентными формами задания поведения конечного автомата Мили.

Слайд:Пример VHDL модели автомата Мили

Следующий VHDL-код реализует поведение конечного автомата, заданного в таблице. Поведение автомата представляется в виде совокупности двух взаимодействующих процессов.
Процесс NS определяет выходной сигнал w и внутренний сигнал NEXT_state, который является входным для процесса REG. Заметим, однако, что в списке чувствительности процесса REG имеется только сигнал clk, который соответствует моментам времени срабатывания автомата.
Для задания состояний автомата в архитектурном теле определяется перечислимый тип t_state. Предполагается, что начальное состояние автомата равно a1. Начальное состояние явно не указывается, так как при инициализации будет взят элемент нижней границы перечислимого типа – это и будет элемент a1.

 Library work;
use work.vv_vls.all;
entity FSM_A is
    port ( z   : in fsm_in_type;
           clk : in bit;
           w   : out fsm_out_type);
end FSM_A;
architecture rtl_a of fsm_a is
type T_state is (a1,a2,a3,a4);
signal NEXT_state : T_state;
signal state : T_state;
begin
    NS : process (state, z)
    begin
        case state is
            when a1 =>
                if (z=z1) then NEXT_state <= a2; w <= w1;
                elsif (z=z2) then NEXT_state <= a4; w <= w5;
                end if;
            when a2 =>
                if (z=z1) then NEXT_state <= a2; w <= w1;
                elsif (z=z2) then NEXT_state <= a3; w <= w3;
                end if;
            when a3 =>
                if (z=z1) then NEXT_state <= a1; w <= w2;
                elsif (z=z2) then NEXT_state <= a4; w <= w4;
                end if;
            when a4 =>
                if (z=z1) then NEXT_state <= a1; w <= w4;
                elsif (z=z2) then NEXT_state <= a3; w <= w5;
                end if;
        end case; end process;
    REG : process(clk)
    begin
        if clk = '1' then
            state <= NEXT_state;
        end if;
    end process;
end rtl_a;

Слайд:Пример VHDL модели автомата Мили

Для входных сигналов автомата в пакете vv_vls определяется перечислимый тип

type fsm_in_type is (z1, z2);

для выходных сигналов в том же пакете определяется перечислимый тип

type fsm_out_type is (w1 , w2 ,w3 ,w4 ,w5);
package vv_vls is
    type fsm_in_type is (z1, z2);
    type fsm_out_type is (w1, w2, w3, w4, w5);
end vvv;
package body vvv is
end vvv;

Многократное изменение синхросигнала clk можно более компактно описать в виде процесса generator. Переменная number задает число тактов. В данном случае число тактов равно 5.

generator : process
variable number : integer := 5;
begin
    for i in 1 to number loop
        clk <= transport '1'; wait for 25 ns;
        clk <= transport '0'; wait for 25 ns;
    end loop;
end process;

При описании схем с памятью выделяют комбинационную часть автомата и память. Описание поведения выполняют в виде совокупности двух взаимодействующих процессов – процесса NS и детализированного процесса REG. Для рассмотренного примера конечного автомата выделение подсхем показано на рисунке.